拓扑材料中对数量子振荡的发现

作者：刘彦昭1,2 王慧超1,2,3 刘海文4 王健1,2,5

(1 北京大学物理学院量子材料科学中心)

(2 量子物质科学协同创新中心)

(3 香港理工大学应用物理系)

(4 北京师范大学物理系)

(5 中国科学院大学 中国科学院拓扑量子计算卓越创新中心)

1930 年舒伯尼科夫(Lev Shubnikov) 和德哈斯(W. J. de Haas) 在铋单晶材料中观测到电阻随磁场的倒数呈周期性变化的规律， 被称为Shubnikov—de Haas(SdH)振荡[1]，这是人类首次发现的量子振荡。由此开始，量子振荡被物理学界所关注，并逐渐成为揭示新奇物理现象的一个重要研究工具。近90年来，研究者在包括金属、金属间化合物、半金属、半导体以及绝缘体在内的诸多材料及介观微结构中都发现了量子振荡[2—8]。按照随磁场变化的规律目前已知的量子振荡可以分为两大类：第一类量子振荡表现为随磁场的倒数呈周期性变化，起源于体系形成朗道能级，代表为磁电阻中的SdH 振荡[9]。目前SdH 振荡已经成为探测材料费米面信息和物性的重要实验手段[4]。参见图1(a，b)。第二类量子振荡表现为随磁场呈周期性变化，起源于介观系统中的准粒子量子干涉，例如环状和柱状结构磁电阻中的Aharonov—Bohm(AB)振荡[10]、Altshuler—Aronov—Spivak(AAS)振荡[11]。参见图1(c，d)。历史上，每一类量子振荡的发现，都源于重要的物理机制，进而揭示出新的物理规律。

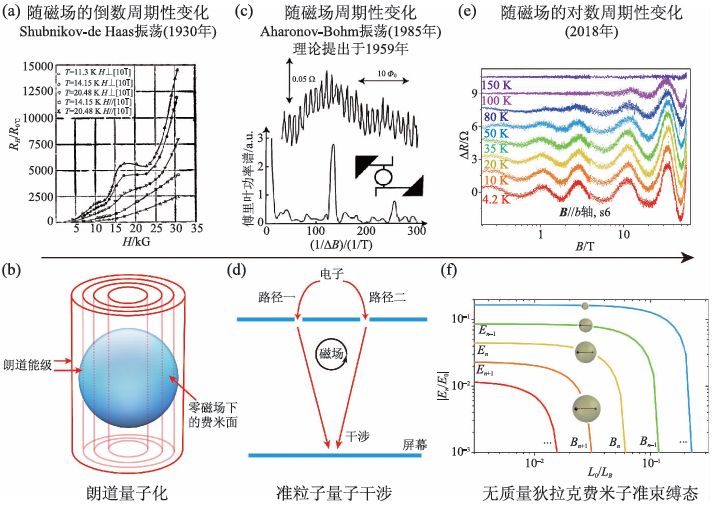
图1 量子振荡家族(a，b)随磁场的倒数周期性变化的量子振荡。典型代表为磁电阻中的Shubnikov—de Haas(SdH)振荡，起源于朗道能级的量子化((a)引自参考文献[1])；(c，d)随磁场周期性变化的量子振荡。代表为磁电阻中的Aharonov—Bohm(AB)振荡和Altshuler—Aronov—Spivak(AAS)振荡，起源于准粒子的量子干涉((c)引自参考文献[10])；(e，f ) 随磁场的对数周期性变化的量子振荡。物理机制为：无质量狄拉克费米子在超临界库仑吸引下形成两体准束缚态。这些满足离散标度不变性的准束缚态在磁场的影响下逐个经过费米面，引起磁电阻的对数周期量子振荡((e，f ) 引自参考文献[12])

近期，我们在高质量的三维层状拓扑材料五碲化锆(ZrTe5)单晶中首次发现了一种新规律的量子振荡——随磁场呈对数周期的磁电阻振荡[12]。近年来，理论工作预言ZrTe5具有非平庸的拓扑能带，从而使得该材料成为了凝聚态物理领域的一个重要研究体系[13]。前期对该材料的研究发现了诸如手性反常效应、反常霍尔效应[14—16]等诸多物理现象。理论和实验工作表明，该体系的物理性质对于晶胞体积十分敏感[12—16]，因而可以表现出丰富的物理特性。为了得到缺陷更少的样品，我们采用了Te 作为自助熔剂的方式来进行样品生长。通过一系列的表征实验，如扫描透射电子显微镜(图2(a)插图)、能量分布谱等，证明了我们的样品具有很高的质量。

由于低载流子浓度和强各向异性，我们的样品具有很小的量子极限，即在很小的外加磁场(约0.2 T)下，该拓扑单晶参与导电的载流子就都处于最低的朗道能级。当磁场超过该材料的量子极限后，发现了包含5 个对数振荡周期的明显结构，并进一步通过在不同样品、不同磁场强度(最高58 T)、不同实验设备中进行多次验证测量，最终确定了这一重要发现。参见图1(e)和图2(a—e)。

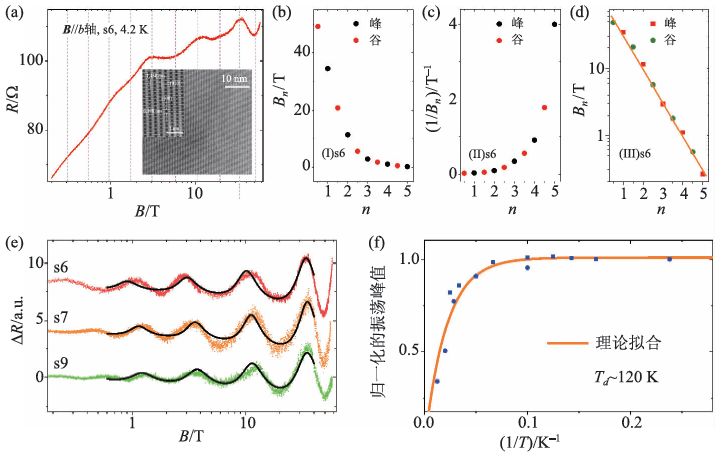
图2 磁电阻中的对数周期量子振荡(a)温度为4.2 K，磁场最高达到58 T下的样品磁电阻信号。插图为样品的高分辨率扫描透射电子显微镜照片；(b—d)振荡的峰和谷对应的磁场值、磁场值的倒数、磁场值的对数和整数与半整数指数的关系；(e)对不同样品对数周期振荡的定量拟合(黑色曲线)；(f)归一化的振荡峰值(n=1)相对于温度的依赖关系。橙色曲线为理论拟合结果，蓝点为振荡峰值(引自参考文献[12])

这一发现不同于以往所有已知的量子振荡。如图2(b—d)所示，当横坐标为整数或半整数指标时，只有纵坐标取振荡的峰值或谷值对应磁场的对数结果，才可以看到明显的线性关系。所以传统的量子振荡理论，无论是考虑了塞曼劈裂的SdH 振荡( 与磁场的倒数呈周期)， 还是AB/AAS 效应(与磁场呈周期)，都无法解释我们发现的对数周期现象。这预示着我们的发现为量子振荡家族增加了一个新的成员，开启了量子振荡的新篇章。此外，相对于已知的量子极限以外的量子态，例如分数量子霍尔态、魏格纳晶体以及密度波相变等[17—21]，对数周期的量子振荡很可能揭示了一种量子极限之外的新型量子态。

对数周期性代表系统呈现出了一种离散标度不变性的特征[22]。标度不变性指体系在任何尺度下都是自相似的，体系不存在特定的特征尺度。离散标度不变性是连续标度不变性破缺的结果，其显著特征是体系的特征尺度满足等比数列。这一特征在动物学、金融危机、地震、湍流等多种研究领域中都有所体现[22]。在经典物理体系里，离散标度不变性存在于非线性方程导致的分形结构中。譬如著名数学物理学家庞加莱提出的庞加莱圆盘模型就是一种满足自相似性的分形结构，参见荷兰著名画家埃舍尔的画作Circle Limit III(图3(a))。对于量子体系，目前已知的只有Efimov三体束缚态表现出离散标度不变的行为[23]。近年来，Efimov 三体束缚态在冷原子实验中得到了观测[24]，进而激发了相关领域极大的研究热情。

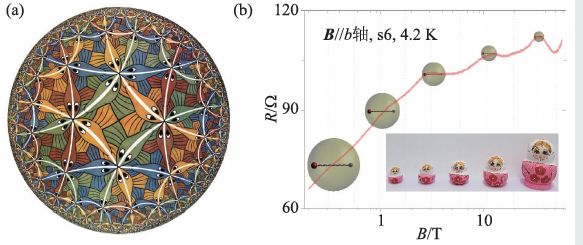
图3 具有离散标度不变性的系统(a)埃舍尔(M. C. Escher)版画Circle LimitIII。代表了一种著名的分形结构——庞加莱(Poincaré)圆盘模型；(b)无质量的狄拉克费米子受到相反电荷的有质量的费米子的库仑吸引形成的两体准束缚态与对数周期量子振荡。插图为俄罗斯套娃，可以看作是狄拉克体系中的离散标度不变性的一个生动类比((b)中对数量子振荡的红色曲线数据引自参考文献[12])

在凝聚态物理领域，狄拉克材料体系为研究离散标度不变性提供了新的平台。相对论量子力学预言当原子序数Z满足不等式Zα>1时(其中α~1/137是自然界中的精细结构常数)，超重原子在强库仑势作用下会发生塌缩现象[25]。超重原子中的超临界塌缩现象是核物理领域的一个非常重要的研究课题，并入选Science 杂志评选出的125 个前沿科学问题[26]。然而这一重要理论预言仍未得到实验的直接证实。狄拉克材料体系中的准粒子满足相对论性方程，并且体系的精细结构常数远大于真空中取值，大大降低了产生超临界坍缩态的临界电荷值，因而可以用来探究原子超临界塌缩现象[27]。在狄拉克材料ZrTe5中，通过对样品的霍尔测量，我们发现样品具有两种有效载流子。其中，轻空穴满足无质量狄拉克方程为相对论粒子且有效光速约为450 km/s，远小于真空中的光速[14]。因此体系的精细结构常数α>1，满足超临界塌缩条件，会形成有限寿命的准束缚态。轻空穴受到电子或带电杂质的库仑吸引而形成相对论量子准束缚态。因样品中的载流子浓度很低，库仑相互作用不能被屏蔽，求解超临界库仑势场中的狄拉克方程就可以发现这些两体准束缚态表现出离散标度不变性。由于满足超临界塌缩条件，这些准束缚态可被看作是不稳定的人造原子的塌缩态。当外加磁场时，随磁场不断增加准束缚态的能级逐个经过费米面，并对费米面处的载流子(也即决定材料导电特性等物性的电子空穴等准粒子)引起散射，参见图1(f)。这些准束缚态在磁场作用下经过费米面而对载流子引起的共振散射会导致电阻发生振荡。数值计算表明，这些满足离散标度不变性的准束缚态经过费米面对应的特定磁场值确实满足等比数列。因此，准束缚态与载流子之间的共振散射导致磁电阻发生对数周期量子振荡。当外加磁场超过量子极限后，通常的SdH 振荡不再出现，因而更有利于观测到这种新的对数周期振荡。在理论的基础上，我们对实验观测到的对数周期量子振荡以及振荡峰值随温度的变化关系进行了拟合，结果如图2(e，f)所示。可以看到数值拟合结果和实验观测的结果十分符合。这种狄拉克体系中的离散标度不变性的发现可以用俄罗斯套娃来做生动的类比，参见图3(b)。我们的研究表明，拓扑材料体系可用于研究超临界原子塌缩现象，该体系中的两体准束缚态具有离散标度不变性等新的特征，拓宽了对超临界原子塌缩的认识。

在此工作基础上，为了证实这种有趣的对数周期量子振荡(离散标度不变性)在具有库仑吸引的狄拉克材料或者拓扑材料中具有普遍性，我们对拓扑材料HfTe5 进行了系统的磁输运研究[28]，发现在HfTe5的纵向磁电阻中同样存在对数周期的量子振荡和离散标度不变性。此外，在样品的霍尔信号中我们也观测到了对数周期的现象，证实了对数周期量子振荡可以普遍存在于狄拉克或拓扑材料中。

对数周期量子振荡的发现不仅是首次在凝聚态体系中通过磁输运的手段探测到了离散标度不变性，而且揭示出一定条件下拓扑材料或狄拉克系统可以作为同时观测原子超临界坍缩及其离散标度不变性的实验平台。因此这一发现可以超出凝聚态物理的范畴，为探究新奇的相对论量子现象提供一个重要的实验平台。

致谢 感谢北京大学物理学院量子材料科学中心谢心澄院士对本工作的理论贡献。

参考文献

[1] Schubnikow L et al. Nature，1930，126：500

[2] Alers P B et al. Phys. Rev.，1956，101：41

[3] GaoWS et al. Phys. Rev. Lett.，2017，118：256601

[4] Zhao Y F et al. Phys. Rev. X，2015，5：031037

[5] Fowler A B et al. Phys. Rev. Lett.，1966，16：901

[6] Xiang Z et al. Science，2018，362：65

[7] Tian M L et al. Nano Lett.，2009，9：3196

[8]Wang J et al. Appl. Phys. Lett.，2008，92：233119

[9] Shoenberg D. Magnetic oscillations in metals. Cambridge University Press，2009. 22-36

[10]Webb R A et al. Phys. Rev. Lett.，1985，54：2696

[11] Al’tshuler B L et al. Jetp. Lett.，1981，33：94

[12]Wang H et al. Sci. Adv.，2018，4：eaau5096

[13] Weng H et al. Phys. Rev. X，2014，4：011002

[14] Li Q et al. Nat. Phys.，2016，12：550

[15] Liu Y et al. Nat. Commun.，2016，7：12516

[16] Liang T et al. Nat. Phys.，2018，14：451

[17] Yu W et al. Sci. Rep.，2016，6：35357

[18] Halperin B I et al. Jpn. J. Appl. Phys.，1987，26：1913

[19] Behnia K et al. Science，2007，317：1729

[20] Analytis J G et al. Nat. Phys.，2010，6：960

[21] Li L et al. Science，2018，321：547

[22] Sornette D. Phys. Rep.，1998，297：239

[23] Braaten E，Hammer H W. Phys. Rep.，2006，428：259

[24] Kraemer T et al. Nature，2006，440：315

[25] Zeldovich Y B，Popov V S. Sov. Phys. Usp.，1972，14：673

[26] Hubble E. Science，2005，309：78

[27] 刘海文，王慧超，王健. 科学通报，2018，63：601

[28]Wang H et al. 2018，arXiv：1810.03109

本文选自《物理》2019年第1期

1. 那棵消失的树—回忆导师张首晟

2. 啁啾脉冲放大技术——从超快激光技术到超强物理世界

3. 超短超强激光驱动新型粒子加速器：机遇和挑战

4. 飞秒激光放大的奠基性发明及其能力边界的突破

5. 《科学》评出2018年度十大科学突破事件

6. 时空克莱因瓶上的热力学——从二维生物的奇妙旅行到共形量子态的路径积分

7. 量子十问之三：量子技术能将人“瞬间”转移到别的星球上吗？| 郭光灿

8. 国际单位制基本量的新定义

9. 超导“小时代”之三十八：走向超导新时代

10. 二维铁电性：一泓秋水映

END