费米－沃克移动（Fermi-Walker transport）是广义相对论中的一种移动。当某一曲线上的矢量场的弗米－沃克导数为零时，称该矢量场沿该曲线作费米－沃克移动。在惯性参考系中，弗米－沃克导数与协变导数一致。
数学表示费米－沃克移动（Fermi-Walker transport）是广义相对论中的一种移动。1当某一曲线上的矢量场的弗米－沃克导数为零时，称该矢量场沿该曲线作费米－沃克移动。在惯性参考系中，弗米－沃克导数与协变导数一致。
假设在曲线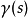
上有一矢量场X，则费米－沃克导数的定义为：
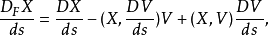
其中V为四维速度，D为黎曼空间中的协变导数。当
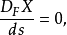称矢量场X沿曲线作费米－沃克移动。沿世界线作费米－沃克移动的空间矢量场是没有空间转动的。
费米 - 沃克分化在洛伦兹流形理论中，费米 - 沃克分化是协变分化的推广。在广义相对论中，相对于帧场中的时间单位矢量场而言，帧场中的类空矢量场的费米 - 沃克导数用于定义非惯性和非旋转帧，通过规定费米 - 沃克衍生品应该消失。在惯性框架的特殊情况下，费米 - 沃克衍生物减少为协变导数。
随着一个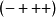
符号约定，这是沿着曲线为矢量场X定义的
：
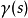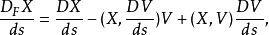
其中V是四速度，D是协变导数。如果
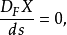
然后，矢量场X是沿曲线传输的费米 - 沃克（参见霍金和埃利斯，第80页）。垂直于闵可夫斯基时空中四速度空间的向量，例如极化向量，在费米 - 沃克运输下体验托马斯进动。
使用费米导数，Bargmann-Michel-Telegdi方程用于外部电磁场中的电子自旋进动可以写成如下：
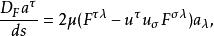
其中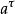
和
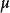极化四矢量和磁矩，
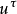是四速电子，
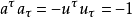和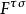
是电磁场强度张量。
共同移动坐标系可以定义与粒子共同移动的坐标系。如果我们采用单位向量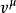
因为在共同移动坐标系中定义一个轴，那么任何用适当时间转换的系统都被称为正在进行费米沃克移动。
本词条内容贡献者为:
刘军 - 副研究员 - 中国科学院工程热物理研究所