宇宙膨胀的本质

在众多宇宙学理论中，最经得起观测检验的成功理论是大爆炸宇宙论。大爆炸宇宙论是1948 年苏联数学家和宇宙学家亚历山大· 弗里德曼（Alexander Friedmann，1888 年—1925 年）的学生俄裔美国科学家伽莫夫（G. Gamow，1904 年—1968 年）等把原子核和基本粒子物理与宇宙膨胀联系起来建立的热大爆炸元素形成理论。这个理论得到了哈勃膨胀、轻元素丰度和微波背景辐射三大观测支柱的强有力支持，称为标准宇宙学（standard cosmology）或者大爆炸宇宙学。

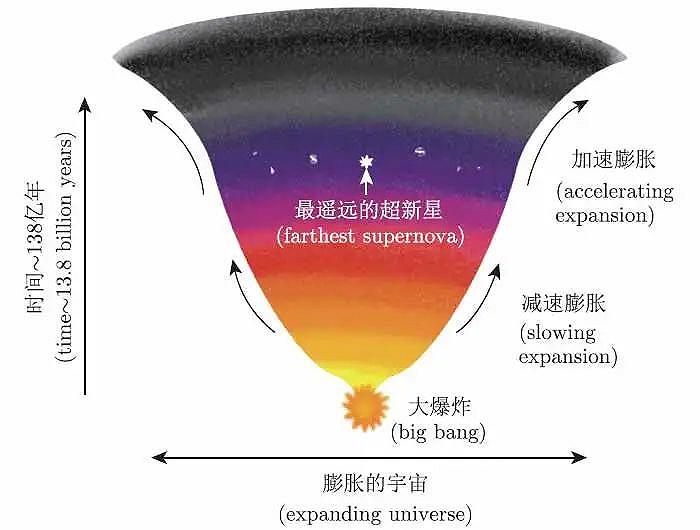
▲ 宇宙大爆炸示意图

膨胀定律

 宇宙的膨胀意味着一对星系之间的固有物理距离随着时间增加，也就是星系之间相互退行。这对星系之间的固有物理距离s(t) （或从我们的位置测量的某个共动点处星系的距离）随时间的变化为

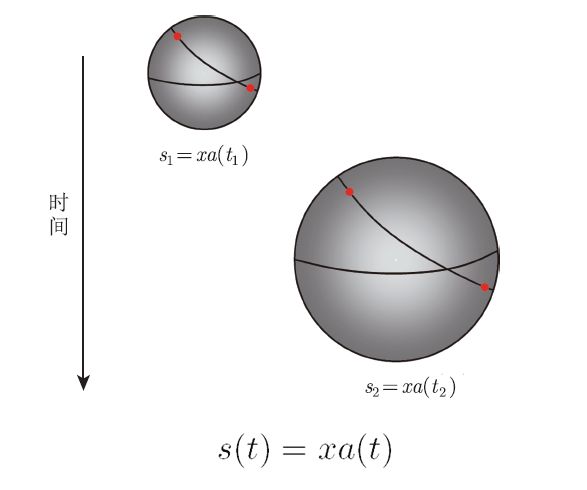
▲ 共动坐标系中两个星系之间的距离随宇宙的膨胀

 其中x 是其共动距离，它是独立于时间的常数，等于今天t0  时刻的固有物理距离。

 在一个星系的观察者测量到另一个星系的退行速度是固有物理距离s(t) 对时间的导数，即

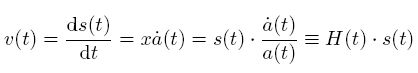
这就是著名的在宇宙任意时刻t 时的哈勃定律。

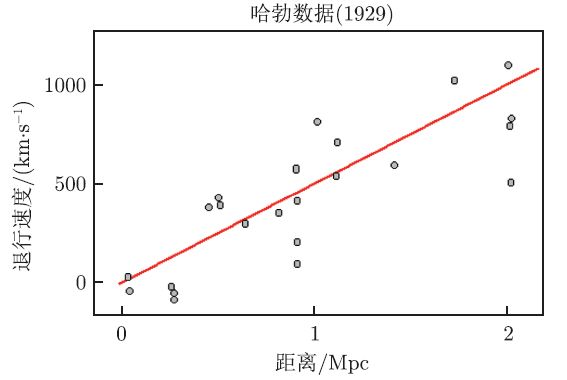
▲ 河外星系的退行速度与距离的关系，即哈勃图(Hubble E. Proceedings of theNational Academy of Sciences of the United States of America, 1929, 15(3):168-173)

 上图展示了天文学家哈勃在1929 年观测到的河外星系的退行速度与距离的关系，即著名的哈勃图，也可以说是天文学史上的第一张哈勃图，只包含几十个星系的样本。哈勃定律并不绝对精确，因为宇宙学原理并不完全适用于邻近的星系，这些星系通常拥有一些随机运动，即所谓的本动速度。但是它确实非常好地描述了星系的平均行为。

 如果观察到的任何天体都在远离我们，乍一看这似乎必须违反宇宙学原理，因为那显然把我们置于了宇宙的中心。然而，事实并非如此。宇宙中每一个或者说任何一个观测者所观测到的天体都以与距离成正比的速度离他远去。宇宙没有中心，但是处处是中心。哈勃定律在任何所谓的宇宙中心都成立。因此，虽然宇宙正在膨胀，但是不论我们想象选择处于哪个星系，宇宙看起来都是一样的。一个常见的比喻是把宇宙想象成烤葡萄干蛋糕或是吹表面上标注点的气球。

▲ 宇宙膨胀示意图——烤葡萄干蛋糕

当蛋糕鼓起（或气球膨胀）时，葡萄干（或点）就会分离。从每一个葡萄干（或点）看，所有其他葡萄干（或点）似乎都在退行，并且距离越远退行的速度越快。因为宇宙中一切物体都彼此飞离，我们可以得出结论：在遥远的过去宇宙中的物体互相更加靠近。事实上，如果往回追溯的宇宙历史足够长，宇宙中的一切都聚在一起，直至最初的爆炸，被称为大爆炸，以大爆炸为起始的宇宙演化模型被称为大爆炸宇宙学，通常也被称为热大爆炸。

膨胀的本质

 宇宙的膨胀意味着什么？

反向思维，我们先讨论它不意味着什么。它不意味着我们的身体会随宇宙膨胀变胖，也不意味着地球绕太阳的轨道会变长，甚至更不表示我们银河系内恒星彼此之间的距离会变大，导致银河系散架。但宇宙的膨胀确实意味着遥远的星系之间的距离越来越远，它们在相互远离。其中的区别是物体的运动是否由它们之间均匀分布的物质的累积引力效应支配。我们身体里的原子不是，它们之间的距离是由化学键的强度决定的，引力不起主要作用，所以分子结构不受膨胀影响。同样，地球在轨道上的运动完全由太阳引力主宰（其他行星的引力贡献较小）。甚至银河系的恒星都在围绕它们自己（和暗物质晕）创造出来的共同的引力势下运动，它们也不会彼此远离。这些特殊环境的共同特点是，它们具有相当大的密度超出（实际上就是密度扰动），与我们推导弗里德曼方程时的物质平滑分布非常不同。

 但是，如果达到足够大的尺度，如几十Mpc（兆秒差距），这时宇宙确实变得均匀和各向同性，星系遵循弗里德曼方程和哈勃定律，彼此分离。正是在这样的大尺度上，宇宙的膨胀才被感觉到，并且宇宙学原理才能适用。

 人们普遍会关注的另一个问题是，远离我们而去的星系退行的速度是否会超过光速？也就是说，基于速度与距离成正比的哈勃定律，如果星系足够远，那么其退行速度是不是能够达到我们想要的那么快，甚至违反狭义相对论？答案是，我们的理论的确预言遥远的天体运动的速度可以比光速快。然而，这种膨胀是空间本身的膨胀运动，如同暴胀宇宙学中的暴胀一样是空间的超光速膨胀。而且没有违反因果关系，因为这些星系之间无法传递信号。此外，也没有违背狭义相对论，因为它针对的是相互通过的物体的相对速度，并不能用来比较遥远的天体的相对速度，或者说狭义相对论描述的是在时空中物体的运动，而不是时空本身的运动。作为类比，想象气球上的一群蜘蛛随气球的膨胀过程。假设蜘蛛移动的最快速度是1cm·s−1。如果任意两只蜘蛛恰好迎面走过，那么它们的最快相对速度是2cm·s−1。现在开始吹气球使其膨胀起来。虽然蜘蛛徜徉在气球表面上的速度仍然不能超过1cm·s−1，但是现在它们脚下的气球在不断膨胀，如果气球膨胀的速度足够快，那么气球上相距很远的蜘蛛很容易以超过2cm·s−1 的速度分开。如果是这样，它们将永远无法互通消息，因为气球把它们分开的速度比它们一起移动的速度还要快，即使是全速（1cm·s−1）。但是，即使宇宙在膨胀，任何两只蜘蛛只要靠得足够近，能够彼此通过，它们的相对速度也必须不超过2cm·s−1。这些相距很远和很近的蜘蛛的运动特征正是哈勃定律的体现。宇宙空间的膨胀就像这个气球，使星系随空间膨胀而互相远离。

来源：科学出版社