原子尺度毛细凝聚的开尔文方程

张田忠

上海大学力学与工程科学学院，上海 200072

摘要：实验表明宏观尺度建立的开尔文方程经适当改造后依然可描述原子尺度水的毛细凝聚现象.

关键词：开尔文方程, 毛细凝聚, 原子尺度

DOI: 10.6052/1000-0992-20-037

在纳米尺度, 小尺寸效应往往导致物质表现出与宏观尺度不同的力学行为, 因此通常认为连续介质模型不再适用。最近，中国科学技术大学近代力学系王奉超与曼彻斯特大学Andre Geim、杨倩等人合作, 通过巧妙的实验设计和精细的理论分析, 表明在宏观连续介质基础上建立的开尔文方程, 经适当改造后依然可描述原子尺度水的毛细凝聚现象, 尽管在这么小的尺度上, 原始开尔文方程中的某些宏观参数已经无法定义. 论文以“Capillary condensation under atomic-scale connement”为题, 于2020 年12 月9 日发表在《Nature》杂志上(Yang et al. 2020).

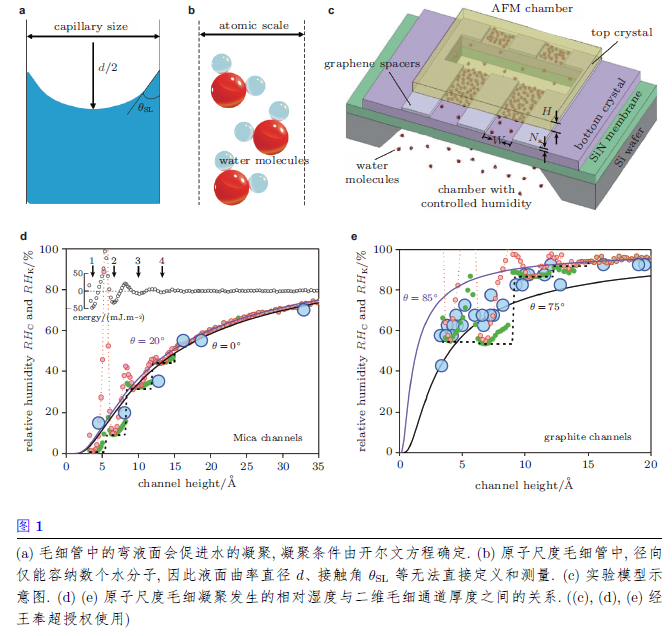
在一定的压力、温度和湿度条件下, 水蒸气会凝聚成液态水. 在毛细管内, 当存在弯液面时(图1(a)), 水蒸气更易凝聚, 这一现象被称为毛细凝聚. 毛细凝聚普遍发生于颗粒物料、多孔介质等的限域空间中, 可显著改变固液界面处的吸附、润滑、摩擦和腐蚀等特性. 因其关联了宏观固液界面润湿与微观分子间力学相互作用, 毛细凝聚成为纳米限域力学的关键科学问题之一(赵亚溥2012, 2014, Wei & Zhao 2007, Wang et al. 2009, Fisher et al. 1981, van Honschoten et al. 2010). 早在150 年前, 英国科学家Thomson (1872) 从理论上描述了毛细管内弯曲液气界面引起的蒸气压变化,建立了描述毛细凝聚条件的数学方程. 该方程后因Thomson 获封开尔文勋爵而被称为开尔文方程,即RHK = exp(-2σ/kbTdρN), 其中RHK 为相对湿度, σ为表面张力, kb为玻尔兹曼常数, T 为温度, d 为液面曲率直径, ρN 为水分子数密度. 此前的研究表明, 当毛细管的尺寸小至4nm 时, 开尔文方程仍可精确描述其内部水的毛细凝聚现象(Fisher et al. 1981). 然而, 当毛细管尺寸进一步缩小, 沿管径方向只能容纳几个水分子时(图1(b)), 连续介质框架下的表面张力、液面曲率（以及接触角等）已经由于水分子的离散排列而无法定义. 因此, 如何描述原子尺度限域内水的凝聚现象成为固液界面力学中的挑战性难题(赵亚溥2012, 2014; Wei & Zhao 2007; Wang et al. 2009; Fisher et al. 1981; van Honschoten et al. 2010). 同时, 虽然原子尺度限域在实际结构(如多孔材料、裂纹尖端等) 中广泛存在, 但在实验室构筑原子尺度限域结构并观察其中水的凝聚现象，也极具挑战性(Kim et al. 2018). 在王奉超等人的研究中, 二维材料被用来构筑纳米通道, 并基于通道壁面变形表征了毛细凝聚. 研究人员将两层云母或石墨用石墨烯条带隔开, 从而在条带之间形成二维毛细通道, 通道的厚度可通过条带石墨烯的层数精确控制(图1(c)). 实验中, 石墨烯条带的层数在1～10 之间, 因此通道的厚度在0:34～3.4 nm, 达到了毛细管尺寸的最小极限. 他们在蒸气环境下测试了原子尺度毛细管的凝聚条件(图1(d) 和图1(e) 蓝色圆圈). 结果显示, 虽然此时弯液面曲率无法直接测得, 但如果用毛细管中接触角与液面曲率的关系、以及宏观尺度的接触角数值近似估计出液面曲率直径(即d=h/cos(θSL), h为毛细管通道厚度), 开尔文方程在定性上还是能对凝聚条件给出很好的描述(图1(d) 和图1(e) 实线). 为了进一步精准给出原子尺度的毛细凝聚条件, 他们在开尔文方程中引入界面能替代表面张力和接触角(即利用了γSV-γSL =σcos(θSL), 其中γSV 和γSL分别为固气和固液界面能). 与实验结果的比较说明, 改造后的开尔文方程能更好地表示原子尺度毛细凝聚条件. 特别地, 改造后的开尔文方程还预测, 在极限尺寸下, 由于固液界面能具有振荡性(图1(d) 黑色圆圈), 毛细凝聚发生的相对湿度也具有振荡性(图1(d) 和图1(e) 红色圆圈及绿色圆圈分别对应刚性壁和柔性壁). 但是, 由于实验中所用的云母和石墨等通道壁的弹性变形, 一定程度上削弱了这一特性, 因此有待进一步通过更为精密的实验确认此现象. 尤其当通道厚度在0.5nm 左右时, 相对凝聚湿度会剧烈震荡, 意味着通道厚度的微小改变可对毛细凝聚产生巨大影响, 这一特性可能在微纳器件设计中具有重要应用.

连续介质理论是人类定量认识宏观自然现象、解决工程实际问题的强有力工具. 纳米科技的发展, 给宏观理论带来了巨大挑战的同时, 也提供了宝贵的发展机遇(杨卫等2002). 连续介质理论在纳米尺度是否仍然适用、什么机制导致其不再适用、或如何改造才能继续适用, 是学术界近年来持续探索的开放课题(赵亚溥2012, 2014). 本世纪初, 清华大学郑泉水曾提出通过混合原子尺度特性与连续介质理论(hybrid atomistic-continuum, HAC) 建立纳米力学模型的理念. 中科院力学所赵亚溥在国内最早开始毛细凝聚的理论和实验研究(Wei & Zhao 2007), 曾指导王奉超步入固液界面力学领域(Wang et al. 2011). 南京航空航天大学郭万林课题组在微纳固液界面力学领域作出了开拓性工作, 提出了水伏效应的概念(Zhang et al. 2018, Yin et al. 2020).

王奉超等人的工作, 不仅拓展了经典开尔文方程的适用范围, 为理解纳米限域毛细凝聚提供了重要的理论依据, 也在拓展连续介质理论解决原子尺度力学问题上迈出了重要一步, 是自上而下发展纳尺度力学理论的典型范例.

来源：力学进展

原文链接：http://mp.weixin.qq.com/s?__biz=MzA3MTIzNzQwMw==&mid=2650343330&idx=1&sn=0d84584d487a2b9a161be817487d156b

电话：（010）86409582

邮箱：kejie@scimall.org.cn