在数学中，卡西米尔不变量，也称卡西米尔元素，是李代数泛包络代数中心的一个判别元素。一个典型的例子是平方角动量算符,这是一个三维卡西米尔元素旋转组。1931年，Hendrik Casimir在刚体动力学描述中定义了卡西米尔不变量。
定义卡西米尔不变量最简单的定义是二次不变量。但是，也可能有卡西米尔不变量高阶，这对应于高阶齐次对称多项式，下面给出了它们的定义。
二次卡西米尔元素假设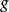
是一个
维空间半单李代数。让B是一个非简并双线性形式，这意味着，对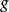 中所有的X,Y,Z，均有下式成立1。
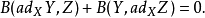
假设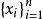
表示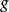 的任意基础形式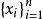， 表示
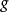关于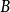
的双重基础形式。对卡西米尔不变量
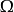的普遍包络代数由下式给出：
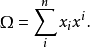
虽然定义依赖于李代数的基础，但很容易证明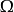 的选择独立性。另一方面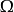， 确实依赖于双线性型B的不变性性，这意味着卡西米尔不变量与李代数
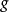的所有元素，以及此通用包络代数中心
。
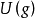卡西米尔不变的线性表示和光滑的行动假定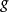
在向量空间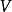
中表示为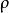
(可能是无限维的)，卡西米尔不变量 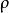的定义是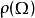
，由V上的线性算子得出下属公式：
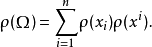
属性独特性对于一个简单的lie代数，每一个不变的双线性形式是Killing形式的倍数，相应的Casimir元素被唯一地定义为一个常数。 对于一般半单李代数，不变双线性形式的空间对于每个简单分量都有一个基向量，因此对于相应的卡西米尔算子的空间也是如此。
与G的拉普拉斯算子如果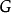
为带有lie代数的李群，那么在
上选择一个不变的双线性形式，
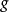对应于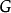
上的一个双不变黎曼度量。然后G上的左不变微分算子在通用包络代数的识别下，g的双线性形式的卡西米尔不变量映射为G的拉普拉斯算子。
特征值考虑到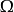 中央在包络代数，它作用于简单模块由一个标量。让
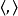是任何双线性对称简形式,我们定义 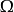。让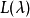
有限维最高重量模块的重量
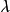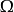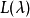。然后卡西米尔不变量 作用于 的常数，
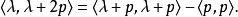
此外，如果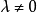
，那么上述常数是非零。然后
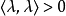且
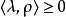，这表明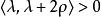
。这个观察的证据起着重要的作用韦尔定理的完整还原性。
本词条内容贡献者为:
刘军 - 副研究员 - 中国科学院工程热物理研究所