运动公理(axiom of motion)是合同公理的另一种表现形式,平面上的运动公理组包括下面六条公理:1.运动把点变为点,把直线变为直线,并且保持结合关系和顺序关系。2.存在这样的运动,把每一个点,每一条直线变为本身,称为恒等运动。3.一个运动之后继以另一运动称为这两个运动的乘积,任意两个运动的乘积仍是运动,对于每个运动必存在另一个运动,使这两个运动的积是恒等运动。4.若运动把某条射线和它的端点变为本身,则射线上的每一点都变为本身。5.若A,B,C是某一图形中不在同一直线上的三点,则存在惟一一个运动,使图形按下面的方式变为另一图形:1) 点A变为已知点A′;2) 点B变为以A′为端点的已知射线h′上的某一点B′,即射线AB变为射线A′B′;3) 点C变为射线h′已知一侧的某一点C′。6.存在运动把线段AB变为BA;也存在运动把∠AOB变为∠BOA。在构造欧氏几何的公理系统时,可采用运动公理组代替与其等价的合同公理组1。
基本介绍在希尔伯特所提出的欧氏几何公理组Ⅰ一Ⅴ中,在组Ⅲ里的“合同”作为基本概念,运动作为派生概念。为了把公理法与克莱因的群论原则结合起来,在希尔伯特之后,就有一些几何专家依照欧几里得在“原本”里的思想,以“运动”为基本概念,而把运动下的对应图形定义为合同图形。关于运动,则用以下10条公理来规定。
公理Ⅲ'1 运动是平面到自身(或空间到自身)的变换,它把点变为点,直线变为直线(平面变为平面)。
公理Ⅲ'2 运动把在直线上的点变为像直线上的点。
公理Ⅲ'3 运动把共线上有序三点变为像直线上同序三个像点。
公理Ⅲ'4存在一个运动把平面上的每个点变成自身(恒等变换)。
公理Ⅲ'5 任意两个运动的乘积仍是一个运动。
公理Ⅲ'6 对于每个运动必存在一运动使得这两个运动的乘积为恒等变换(逆运动)。
公理Ⅲ'7若运动把某条射线和它的顶点变为自身,那么射线上各点都变为自身。
公理Ⅲ'8 设在一个平面上有两个点P与Q,和以它们为顶点的两射线PA和QB,以及由这两条为射线所在直线为边缘的半平面α和β,那么存在唯一运动,把点P变为点Q,射线PA变为射线QB,半平面α变为半平面β。
公理Ⅲ'9 存在运动把线段AB变为线段BA。
公理Ⅲ'10存在运动把角∠(h,k)变为角∠(k,h)。
上述10条公理合成一个公理组Ⅲ',叫做运动定理。其中公理Ⅲ'9和Ⅲ'10又叫做反射公理2。
相关定理由公理Ⅲ'1-3可推出(以下定理的证明请参考相关文献2):
定理1 每个运动都把线段变为线段,射线变为射线,半平面变为半平面。
在组Ⅰ、Ⅱ的基础上,组Ⅲ'与Ⅲ是等价的。下面举例说明。
定理2 设A和B是直线a上的两个点,又A'是同一直线或另一-条直线a'上的点,则在直线a'上点A'的任意指定的一侧存在唯一一点 B',使得线段AB= A'B'。
证明: 设点A'是直线a'上一点,并指定某一侧为射线A'B' ,以直线a,a'为边缘的半平面分别为α和α',由公理Ⅲ'8可知,存在一个运动f,使得点A变为点A' ,射线AB变为射线A'B',点B变为射线A'B'上的一点B',即线段AB变为线段A'B',就是说AB≡A'B'。现证点B'是唯一的。以直线a、a'为边缘的另一对半平面分别记β和β',也存在一个运动f',把点A变为点A' ,射线AB变为射线A'B',β变为β',而点B变为点B"。由公理Ⅲ'6知,存在f的逆运动f-1,它把射线A'B'变为AB;又由公理Ⅲ'8知,f'f-1也是一个运动,它把射线A'B'变为射线A'B',因此根据公理Ⅲ'7,A'B' 上所有点均不变,从而 f'f-1(B')) = B',但f'f-1(B') = B",故B' = B"2。
定理3图形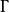 的合同关系满足:
的合同关系满足:
1.反射性: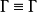 。
。
2.对称性:若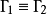 ,则
,则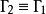 。
。
3. 传递性:若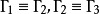 ,则
,则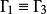 。
。
推论 若线段A'B'= AB,A"B"= AB,则A'B' = A"B”。
定理4 设AB与BC是直线a上而无公共内点的线段,A'B'与B'C'是直线a'(或a=a')上两条无公共内点的线段,若AB= A'B',BC= B'C',则AC= A'C'2。
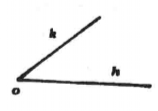
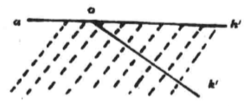
定理5 如图1所示,设平面α上给定一个角∠(h,k),在同一个或号一个平面α'上给定直銭a',而且在平面α'上指定了直线a'的一侧,设h'是直线a'上从一点O'出发的射线,那么在平面α'上存在着唯一的一条射銭k',使得∠(h,k)合同于∠(h',k');而且∠(h',k')的所有内点都在直线a'所指定的那一侧,并且毎个角都与它自身合同,即∠(h,k)= ∠(h',k');∠(h,k)= ∠(h,k)。
定理6 如果两个三角形△ABC与△A'B'C'之间满足:AB≡A'B',AC≡A'C',∠BAC≡∠B' A'C',则∠ABC≡∠A'B'C',∠ACB≡∠A'C'B',BC≡B'C'。2
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所