逆位似点(inverse homothetic points)是与两圆位似点相关的一对点，指一个圆与两已知圆分别相切于A和A′，S为两已知圆的位似中心，若直线AA′通过S，且A，A′不是对于S的位似点，则A和A′称为两已知圆的位似中心的逆位似点1。
基本介绍当我们研究与二已知圆周相切的圆周时，下列的概念起着很大的作用：两点A及A'分别在两圆周O及O'上，而这两圆周的一个相似中心为S，假如直线AA'通过这个相似中心，而且点A及A'不是关于相似中心S的位似点，则我们把这两点A及A'叫做这二圆周的一个相似中心S的逆位似点。
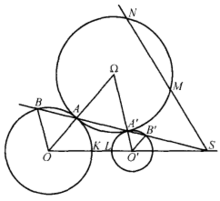
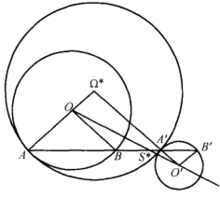
如图1的两点A及A' ，同样两点B及B'，都是关于外相似中心S的逆位似点。(而于图2的两点A及A'，两点B及B' ，是关于内相似中心S*的逆位似点)2
逆位似点的性质逆位似点具有下列性质2。
定理1 自二圆周外相似中心到这二圆周上关于这相似中心的任意二逆位似点的距离的乘积，恒有一个同一数值(按绝对值及其符号)。
关于内相似中心的逆位似点，也有同样的性质。
证明 设A及A'分别为二圆周O及O'上关于其外相似中心S(图1)的任意的逆位似点，用B及B'表示直线SA与圆周O及O'的第二交点，用p及p'表示点S关于圆周O及O'的幂，用
表示圆周O及O'的相似系数，我们有
与点A及A'的选择无关，关于内相似中心的逆位似点(图2)，本定理用同样的方法可以得到证明。
常数积
常叫做二圆周的共同幂，由于S是二圆周的外或内相似中心，常将这个常数积叫做外或内共同幂。
定理2 与二已知圆周相切的任意圆周，其切点为二逆位似点；假如与二已知圆周皆为外切或皆为内切，则二切点关于外相似中心为逆位似点；如与二已知圆之一外切而与另一圆周内切，则二切点关于内相似中心为逆位似点2。
当二已知圆周相等时也不作特别的说法(图3)，即当没有外相似中心时，假如二相等圆周上的二点A，A'联结而成的直线AA'与连心线平行，且半径OA及O'A'不平行，这时我们仍说二点A及A'“关于外相似中心为逆位似点”。
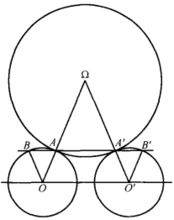
证明 设任意圆周Ω与二已知圆周O及O'分别相切于点A及A'，且同为外切，直线AA'与圆周O及O'的第二交点为B及B'(图1)，因为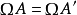
，则
∠OAB =∠ΩAA'=∠ΩA'A =∠O'A'B’=∠O'B'A'
所以，半径OA及O'B'平行，即点A及B'为关于外相似中心的位似点，而点A及A'为其逆位似点。
如与二已知圆周同为内切，或如圆周Ω*(图2)与二已知圆周之一内切而与另一圆周外切，本定理同理可以得到证明。
系 外(内)相似中心关于与二已知圆周同为外切或同为内切(与其一为内切而与其他为外切)的所有圆周，有同一的幂，它等于关于已知圆周的外(内)共同幂。
与定理1和2相对照，即可导出。
定理3 通过二圆周上二逆位似点且与一圆周相切的圆周，与另一圆周亦必相切。
证明 设圆周Ω(图1及3)通过二已知圆周O及O'上的二点A及A'，这二点关于外相似中心为逆位似点，且圆周Ω与圆周O外切于点A。
因为点A及A'为关于外相似中心的逆位似点，则
∠OAB =∠O'B'A'=∠O'A'B'，
因为圆周Ω与圆周O相切于点A，则
∠OAB =∠ΩAA'=∠ΩA'A，
所以∠O'A'B' =∠ΩA'A，因此推知点Ω，A'，O'在一直线上，则得圆周Ω与圆周O'相切于点A'。
本定理的另外一种情形用这样的方式亦可得证2。
本词条内容贡献者为:
王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所