决定性公理(determinstic axiom)是集合论的一条重要公理，在现代描述集合论中无穷对策具有重要的作用。考虑二人对策：设M={0，1，…，m-1}，参赛者Ⅰ和Ⅱ轮流在M中选取n个数，得到结果序列，设为〈p1，q1，p2，q2，…，pn，qn〉，称为一个结局。一个结局的集合S被事先给出并且为Ⅰ和Ⅱ知道.最后，若〈p₁，p₂，…，qn〉∈S，则Ⅰ获胜；否则〈p₁，p₂，…，qn〉∉ S，则Ⅱ获胜，把这种对策记为GS，许多二人参赛的智力游戏，如下棋，都能在适当地选择M，n和S后，以这一抽象的形式被数学地表示，Ⅰ的一种必胜策略是指一规则：在Ⅰ的每一步，该规则可以根据双方在此以前的取法告诉Ⅰ这一步该怎样取，最终使Ⅰ获胜，类似地，可定义Ⅱ的必胜策略，在n是有穷的情况下，容易证明Ⅰ或Ⅱ必然有一个必胜的策略，也就是说对策是决定的，但在n是无穷时，对策是否是决定的就不再是明显的事实，决定性公理是：对于每个结局集S，GS是决定的，这里S⊆{〈p₁，q₁，p₂，q₂，…，pn，qn，…〉|pn，qn∈w}1。
基本介绍决定性公理是公理集合论用语。可添加到公理集合论ZF系统中去的一条公理，简记为AD。其内容为：对于每一个集合S⊆N↑N，对策G(S)都是决定性的。其中的N是自然数集，N↑N是{f| f：N→N}，G(S)是与集合S相关的二人对策，所谓二人对策G(S)，是指：对局者甲和乙依次选取自然数：a0，b0，a1，b1，…(甲选取a0，a1，…;乙选取b0，b1，…)，是一个函数g：N→N，即g∈N↑N，如果g∈S，则对局者甲胜，否则为对局者乙胜。如果甲(或乙)按照某种策略g取值一定能获胜，则称甲(或乙)有必胜策略，并称对策G(S)是决定性的。决定性公理与选择公理(简记为AC)是彼此冲突的。可以证明，在公理集合论ZFC(即ZF+AC)系统中，决定性公理不成立。反之，如果把决定性公理添加到公理集合论ZF系统中去(记作ZF+AD)，则有某些弱的选择公理成立。例如，在ZF+AD系统中，实数的非空子集的每一个可数簇都有一选择函数。
相关说明及结论对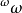
的每一个子集A，我们定义下面的游戏GA：甲、乙二人对局，甲选取自然数a0，乙选取自然数b0，接着甲取数a1，乙取数b1，从而形成二无穷序列
甲
乙
若所得结果序列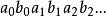
在A中，则甲胜，否则乙胜。甲的策略σ为一函数，使得对任何n，
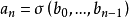，乙的策略
也为一函数，使得对任何n，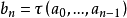
，
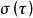对甲(乙)来说是必胜策略，若甲(乙)运用它作游戏GA时不管乙(甲)如何着法，他必胜。
游戏GA称为决定的，若甲、乙二人中有一人必有必胜策略。
决定性公理(Axiom of Determinateness)
AD：对每一个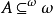
，游戏GA是决定的；
决定性公理AD与选择公理AC不相容2。
定理 若所有实数集是良序的，则存在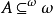 ，使得GA是非决定的。
证明 设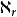
为一无穷基数使得
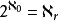，运用超穷递归构造集合
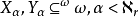，使得
[1]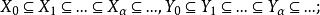
[2]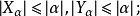
[3]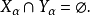
令
，则A是非决定的2。1
因为策略数为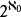
，所以令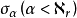
是所有策略的枚举。设
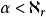，假定对所有
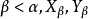已确定。（1）若lim α，则令
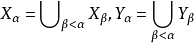；（2）若suc(α)，令α=β+1，则
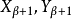如下确定：若甲使用策略
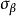，而乙任意地以b={b0，b1，…}与甲游戏，则共有 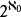个不同的对局，以
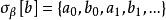表示其中任意一个对局。因
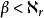，故存在
使得
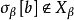。由假定，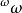
已被良序。因此我们可选取有此性质的最小b，并且
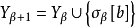。同样地，若乙使用策略
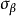，则存在a使得
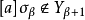，这里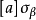
表示已使用策略 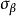而甲取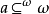
中的元与之游戏的对局。这时选取这样的最小a令
。
令 ，则我们获得游戏GA，因为任意策略σ是
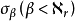中的一个，由
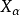的构造可知，甲、乙二人都无必胜策略。
决定性公理与弱选择公理之一——可数选择公理是相容的。
可数选择公理(Countable Axiom of choice)：非空集的每一个可数族有选择函数。
定理 若决定性公理成立，则实数的任一个非空子集组成的可数族有选择函数。
证明 设X={X0，X1，...}是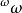 的非空子集组成的可数族，则X有选择函数。事实上，若甲玩a={a0，a1，...}．乙玩b={b0，b1，...}，甲没有决胜策略，因为一旦甲取数a0以后，乙能容易地玩b使
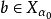，乙玩b={b0，b1，…}，甲以{a0，0，0…}与之对局，则结果序列a0b0…
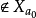。可见乙有必胜策略
，于是在X上定义函数f，使得f(Xn)是乙运用 策略时，对抗甲的{n，0，0，…}的那个b2。
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学