在数学中，数学巧合指的是两个数学表达式的值极为接近，却未有任何理论解释的现象。例如，2的10次方非常接近于整数1000。
工程学中有时会利用数学巧合，使用某个表达式去近似计算另一个表达式。
有理数近似在某些情况下，用简单的有理数近似可以极其逼近某个无理数。大部分这类巧合可以用无理数的连分数表示法来解释；但是，若要进一步探究连分数展开中出现的不寻常大项，则有时是无法通过理论解释的。1
π圆周率π的第一个连分数近似——[3; 7] = 22/7 = 3.1428...，由阿基米德给出，误差约为0.04%。π的连分数近似的前三项——[3; 7, 15, 1] =355/113= 3.1415929...，由祖冲之给出，精确到小数点后6位。π之所以会在连分数近似的第三项达到如此高精确度是因为连分数表示[3; 7, 15, 1, 292, ...]中的下一项——292——是不寻常的大项。
位于圆周率小数点后第762位的连续的六个9。对于一个随机选取的正规数，能在小数点后762位就出现一组特别的六位数字的概率只有0.08%。π是否是一个正规数还不为人知。
e1828这一串数字在e= 2.718281828....的前9位中就连续出现了两回。
e的前50万位中出现了一串“99999999”（8个9）。
数字表达式包含 π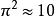
；误差约为1.3%，可以通过ζ函数的公式
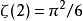来理解这个近似。
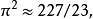；误差约为0.0004%。
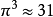；误差约为0.02%。
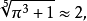；误差约为0.004%。
对数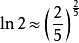
，误差约为0.00024%。
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学