在数学中，极性集是位势论里的一个重要概念，地位有比零测度集之于测度论，极性集合在位势论中也代表一类特别“小”的集合，通常可以忽略不计。
定义
里的极性集可以如下定义：
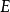是极性集当且仅当存在非常数的次调和函数，使得1
在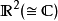
的情形，可以用容度定义极性：集合
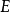被称作极性的（polar），当且仅当它的容度为零。
若将定义中的次调和函数改为多重次调和函数，得到的集合称作多重极性集。
性质中的单点集合是极性的
可数个极性集的联集也是极性的
极性集的勒贝格测度为零
极性集必然是完全非连通的
最后两点并非充分条件，例如康托尔集合测度为零而且完全非连通，但它不是极性的。
本词条内容贡献者为:
任毅如 - 副教授 - 湖南大学