在拓扑学和数学的其他相关领域里，拓扑空间 X 的子空间是指在 X 中子集 S 及在 S 上赋予的由 X 的拓扑所诱导的拓扑．这个诱导出来的拓扑叫做 X 的拓扑在 S 上的相对化拓扑，也叫子空间拓扑、“自然拓扑”．
定义给定一拓扑空间 (X,τ) 和一 X 内的子集 S ，于 S 上的子空间拓扑被定义为
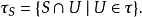亦即， S 的子集于子空间拓扑中为开集当且仅当其为 S 和一于 (X,τ) 内的开集的交集。若 S 被设上子空间拓扑，则其本身即为一拓扑空间，并被称之为 (X,τ) 的子空间。除非有额外叙述，一般拓扑空间的子集都会假定设有一子空间拓扑。
若 S 为 (X,τ) 内的开集、闭集或稠密集，则分别称 (S,τS) 为 (X,τ) 内的一开子空间、闭子空间或稠密子空间。
另外，也可以定义 X 内的子集 S 的子空间拓扑为会使得内含映射
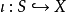为连续的最弱拓扑。
更一般地，设 i 为一由集合 S 至拓扑空间 X 的单射，则于S上的子空间拓扑即为定义为 i 为连续的最弱拓扑。此拓扑的开集恰好会是 i(U) 的其中一个，其中的 U 为 X 内的开集。 S 因此同胚于在 X 内的值域（也是带子空间拓扑），且 i 会被称之为拓扑嵌入。1
例子给定一具一般拓扑的实数，其自然数（实数的一子空间）的子空间拓扑会是一个离散拓扑。
有理数Q做为一个R的子空间，不带有离散拓扑（点 0 在Q内不是开集）。
令S= [0,1) 为实线R的一子空间，则 [0,½) 在S内为开集，但在R内则不是。相似地，[½, 1) 在S内为闭集，但在R内则不是。S为其自身的开子集和闭子集，但做为R的子集则两者皆不是。2
本词条内容贡献者为:
任毅如 - 副教授 - 湖南大学