如果把上述距离的条件1改为ρ(x,y)≥0且ρ(x,x)=0，则称ρ为R上的拟距离。
简介度量空间度量空间亦称距离空间，是一种拓扑空间，其上的拓扑由距离决定。度量空间是弗雷歇(Frechet,M.-R.)于1906年引进的，它是现代数学中的一种基本而重要并且非常接近于欧几里得空间的抽象空间，也是泛函分析的基础之一。
设R是一个非空集合，ρ(x,y)是R上的二元函数，满足如下条件：
1.ρ(x,y)≥0且ρ(x,y)=0⇔x=y;
2.ρ(x,y)=ρ(y,x);
3.(三角不等式)ρ(x,y)≤ρ(x,z)+ρ(y,z)，则称ρ(x,y)为两点x,y之向的距离，R按距离ρ成内度量空向或距离空向，记内(R,ρ)。
设A是R的子集，则A按R中的距离ρ也成内度量空间，称为R的（度量）子空间。
定义如果把上述距离的条件1改为ρ(x,y)≥0且ρ(x,x)=0，则称ρ为R上的拟距离。
相关概念当ρ(x,y)=0时，记x~y，~是R上的一个等价关系，记商集（即等价类全体为D=R/~，在D上作二元函数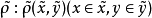
，则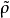
是D上的距离，而(D,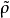)称为R按拟距离ρ导出的商（度量）空间。
度量空间(R,ρ)中的子集A称为有界的，如果对x0∈R，存在常数M，使ρ(x0,x)≤M对A中的一切x成立。
设x0∈R，r>0，则称集合{x|x∈R,ρ(x,x0)