可允许拓扑是一种局部凸拓扑，也可称为集类?上的一致收敛拓扑，而相应的有界集族?称为可允许集族。
简介可允许拓扑是一种局部凸拓扑。
设(X,Y)是对偶线性空间，?是Y中的有界集族，且并U{A|A∈?}的线性包是Y，即Y是U{A|A∈?}张成的线性空间，对每个A∈?，定义半范数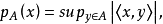
则由半范数族{pA(x)|A∈?}确定的X上局部凸拓扑T?，称为关于对偶线性空间(X,Y)的一个可允许拓扑，或在集类?上的一致收敛拓扑，而相应的有界集族?称为可允许集族。
令?是Y中有限集全体形成的集族，则有T?=σ(X,Y)，因而弱拓扑是可允许的。1
局部凸拓扑局部凸空间是最重要的一类拓扑线性空间。设E是拓扑线性空间，如果E中存在均衡凸集组成的零元的领域基，就称E是局部凸的拓扑线性空间，简称局部凸空间，而E的拓扑称为局部凸拓扑。
半范数半范数是范数的一种推广，其比范数的要求弱（半范数比范数少一个条件：使半范数值为0的元素不一定是0元素），范数一定是半范数。局部凸线性空间的拓扑可以由一族满足分离公理的半范数来确定。
设p是定义于线性空间X上的非负实值函数，满足：
（1）
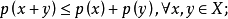
（2）
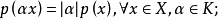
则称p是X上的一个半范数，X称为赋半范线性空间。
注：半范数与范数的不同之处在于，由p(x)=0不能推出x=0.（使半范数值为0的元素不一定是0元素）。
本词条内容贡献者为:
李嘉骞 - 博士 - 同济大学