哈密顿方程组（Hamilton system）是与欧拉-拉格朗日方程组等价的一阶微分方程组。
简介哈密顿方程组是与欧拉-拉格朗日方程组等价的一阶微分方程组。
以最简变分积分J(y)为例，做变换
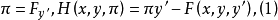则J(y)相应的二阶欧拉-拉格朗日方程可化为以y,π为未知函数的一阶微分方程组
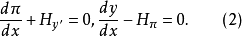正是两个未知函数的变分积分
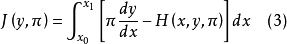的欧拉-拉格朗日方程。
一般地，设一元向量函数的变分积分的拉格朗日函数 F(x,z,p) 满足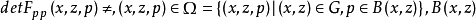
是 RN 中的开集，
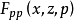是以
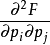为元素的 N×N 矩阵，做勒让德变换
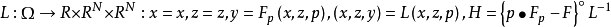令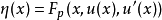
，η 称为矩，二阶欧拉-拉格朗日方程转换化为一阶方程组
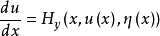
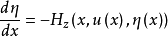这个方程组称为典范方程组或哈密顿方程组，H 称为哈密顿函数。
性质光程函数 S满足哈密顿-雅可比方程
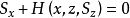哈密顿方程组是变分积分
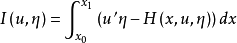或
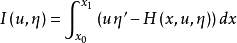的欧拉-拉格朗日方程，若哈密顿函数不显含 x ，则 H 是运动常量，即沿任何解u(x)，H 是常数。1
本词条内容贡献者为:
杨荣佳 - 教授 - 河北大学